Simetria

Se uma função satisfaz $f(x) = f(-x)$, diz-se que $f$ é uma função par. Por sua vez, se $f$ satisfaz $f(x) = -f(x)$, diz-se que $f$ é uma função impar.

EX: $x^2$ é uma função par pois:

$$f(x) = x^2 = \begin{cases} x^2, se x \ge 0 \\ (-x)^2 = x^2, x <0 \end{cases}$$

Por sua vez $x^3$ é impar.

Função par

Satisfaz a $f(x) = f(-x)$, para todo $x$ em domínio.

EX: $x^2$ é uma função par e $x^3$ é uma função ímpar

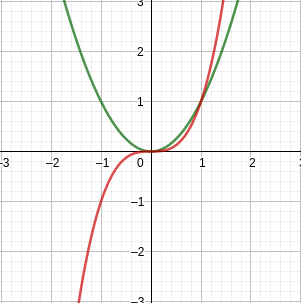
VERIFICANDO: sejam $a$ e $b$, tais que $a=x$ e $b=-x$, fazemos $f(a)$ e $f(b)$:

$$f(a) = a^2$$ $$f(b) = b^2$$

$a^2$ e $b^2$ são positivos para qualquer valores reais, assim:

$$a^2 = x^2$ $

$$b^2 = (-x)^2 = x^2$$

Ou seja, $f(a) = f(b)$, assim, $f(x) = x^2$ é uma função par.

Usando o mesmo procedimento para $f(x) = x^3$:

$$f(a) = a^3$$ $$f(b) = b^3$$ $${a^3} = {a}^2a \iff \\ x^2x\iff \\ x^3$$ $${b^3} = {b^2} b \iff \\ x^2x \iff \\ -x^3$$

Ou seja, $f(a) = -f(b)$, portanto $f(x) = x^3$ é uma função ímpar.

OBS: o procedimento deve ser válido para todo $x$ do domínio.

Função crescente e decrescente

Diz-se que $f(x)$ crescente em um intervalo $I$ quando:

$$f(x_1) < f(x_2) \text{, quando } x_1 < x_2$$

Por sua vez, a função é decrescente quando:

$$f(x_1) > f(x_2) \text{, quando } x_1 < x_2$$

Graficamente temos a representação como no esquema abaixo:

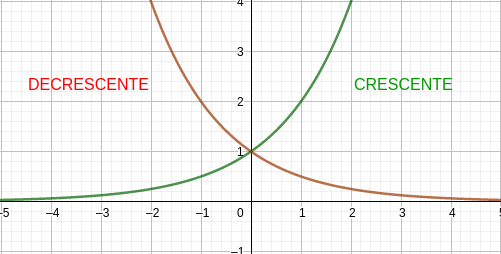
Tipos de função

Modelos lineares de uma função

Dizemos que um modelo representa uma função linear quando seu gráfico corresponde a uma reta ou quando pode ser representado na forma:

$$f(x) = mx + n$$

Em que $m$ e $n$ são constantes reais.

Modelos polinomiais

Um polinômio é uma representação algébrica que segue o formato $P(x)$ tal que:

$$P(x) = a_0x^0 + a_1x^1 + a_2x^2 + ... + a_nx^n$$

Em que $a_0$, $a_1$, $a_2$, …, $a_n$são denominados coeficientes números reais. uma função é dita polinomial se puder ser representada por $P(x)$ arbitrário.

O grau do polinômio equivale ao valor máximo de $n$ presente na expansão. Vale resaltar que $n \in \N$.

Função constante: $n = 0$

$$f(x) = a_0$$

Função afim: $n = 1$

$$f(x) = a_0 + a_1x$$

Função de 2º grau: $n = 2$

$$f(x) = a_0 + a_1x + a_1x^2$$

Função de 3º grau: $n = 3$

$$f(x) = a_0 + a_1x + a_1x^2 + a_3x^3$$

Funções potência

São aquelas representadas por polinômios os quais $a_0, a_1, a_2, … , a_{n-1} = 0$, ou seja, o único elemento não nulo é $a_n$, além disso $a_n = 1$.

EX:

$$f(x) = x^2 \\ f(x) = x^3 \\ f(x) = x^5$$

Funções racionais

São representadas pelo quocinete $P(x)$ e $Q(x)$ tal que seu domínio será $Q(x) \ne 0$, assim:

$$f(x) = \frac{P(x)}{Q(x)}, Q(x) \ne 0$$