você está na primeira aula | proxima aula

Digitado por $\color{black}\text{ Diefesson de Sousa Silva - 471842}$

Limites e derrivadas

Motivação

Problemas que envolvem cálculos de retas tangentes com aproximações por retas secantes são recorrentes em inúmeras áreas do conhecimento nas ciências exatas, como física clássica, mecânica, otimização e etc.

Problemas clássicos de física que envolvem aproximação de retas tangentes são: cálculo de velocidade, aceleração, força, trabalho, energia e etc.

Vamos relembrar um problema clássico de cinemática

Suponha um veículo que percorre uma distância $x$ em metros em $t$ segundos. Observe a seguir:

Distância percorrida	Tempo
$x = 0 \text{ m}$	$t = 0 \text{ s}$
$x = 2 \text{ m}$	$t = 2 \text{ s}$
$x = 4 \text{ m}$	$t = 3 \text{ s}$
$x = 6 \text{ m}$	$t = 3,5 \text{ s}$
$x = 8 \text{ m}$	$t = 4 \text{ s}$

Observe as perguntas a seguir:

1) Qual a velocidade média do veículo após $8 \text{ s}$?

R: neste caso, podemos apelar para a relação $V_m = \frac{\Delta S}{\Delta t}$

$ V_m = \frac{8\text{ m}}{4 \text{ s}} = 2 \text{ m/s} $

2) A velocidade do veículo é constante ou variável?

R: veja a velocidade média nesses casos

$V_m(0 \text{ até } 2) = \frac{2 \text{ m}}{2 \text{ s}} = 1 \text{ m/s}$

$V_m(2 \text{ até } 4) = \frac{2 \text{ m}}{1 \text{ s}} = 2 \text{ m/s}$

$V_m(0 \text{ até } 4) = \frac{4 \text{ m}}{3 \text{ s}} = 1,333… \text{ m/s}$

Perceba que, em diferentes trechos, a velocidade média é alterada.

Usamos $\color{red} \text{limites}$ e $\color{red} \text{derrivadas}$ para representar essas variações.

O limite de uma função

Vamos analisar o comportamento de uma função definida por $f(x) = x^2 - x + 2$ para valores próximos de $x = 2$, porém não iguais a $2$.

$\bold{x}$	$\bold{f(x)}$	$\bold{x}$	$\bold{f(x)}$
$1$	$2$	$3$	$8$
$1,5$	$2,75$	$2,5$	$5,75$
$1,8$	$3,44$	$2,2$	$4,64$
$1,9$	$3,71$	$2,1$	$4,31$
$1,99$	$3,97$	$2,01$	$4,03$

Veja graficamente o comportamento da função:

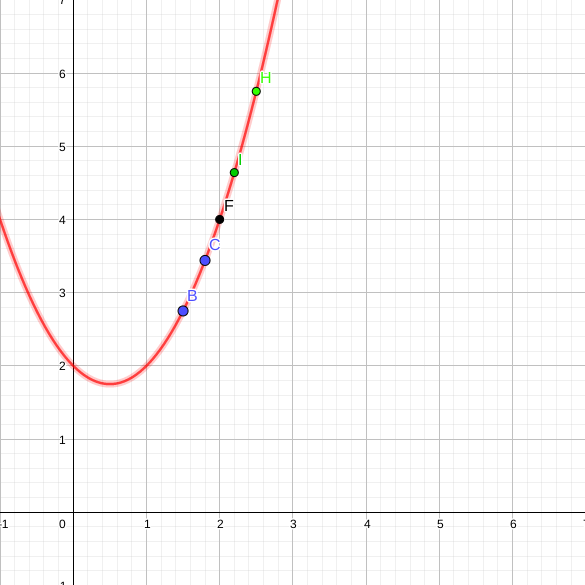
IMPORTANTE: veja que não precisamos calcular $f(2)$ para ver aproximadamente a aproximação $f(2) = 4$, ou seja, podemos visualizar o conceito que o $\color{red} \text{limite}$ da função $f(x)$ quando $x$ está próximo de $2$ como:

$ \lim_{x \rightarrow 2} f(x) = 4 \text{ ou } \lim_{x \rightarrow 2} (x^2 - x + 2) = 4 $

DEFINIÇÃO: suponha que $f(x)$ seja definido quando $x$ está próximo do ponto $a$, sem necessariamente, existir o ponto $a$. Então:

$ \lim_{x \rightarrow a} f(x) = L $

E dizemos “o limite de $f(x)$, quando $x$ tende a $a$ é igual a $L$, se pudermos tornar os valores de $f(x)$ arbitrariamente próximos de a, mas não necessariamente, resolvendo $f(a)$.

Como determinar o valor da função:

$f(x) = \frac{x^2 - 1}{x -1}$

Próximo de $x = 1$, sabendo que $f(x)$ não pode ser calculado?

$\bold{ x < 1}$	$\bold{f(x)}$	$\bold{x > 1}$	$\bold{f(x)}$
$0$	$1$	$2$	$3$
$0,5$	$1,25$	$1,5$	$2,5$
$0,8$	$1,5$	$1,2$	$2,2$
$0,9$	$1,8$	$1,1$	$2,1$
$0,99$	$1,9$	$1,01$	$2,01$
$0,999$	$1,999$	$1,001$	$2,001$
$0,9999$	$1,9999$	$1,0001$	$2,0001$