aula anterior | próxima aula

Digitado por $\color{black} \text{Diefesson de Sousa Silva - 471942}$

Limites(continuação)

Nas últimas aulas, verificamos a comportamento dos limites pela $\color{red} \text{esquerda}$ e pela $\color{red}\text{direita}$ de uma função. Relembrando:

Limite lateral pela direita de $f(x)$:

$\lim_{x \rightarrow a^+}f(x) = L_1$

Limite lateral pela esquerda $f(x)$:

$\lim_{x \rightarrow a^-}f(x) = L_2$

Definimos que, quando $L_1$ e $L_2$, a função $f(x)$ terá limite em $x = a$ se, e somente se:

$\lim_{x \rightarrow a^+}f(x) = \lim_{x \rightarrow a^-}f(x)$

Ou seja:

$\lim_{x \rightarrow a}f(x) = L_1 = L_2$

Limites infinitos

Vamos observar o que acontece com funções reais próximas de um ponto de indeterminação.

EX

$f(x) = \frac{1}{x^2}$

Veja que próximo de $x = 0$, bilateralmente, há a seguinte condição:

1.

$\lim_{x \rightarrow 0^+}f(x) = +\infty (\text{infinito})$

Veja que $f(x) = \dfrac{1}{x^2}$ tende a um valor muito grande e positivo quando $x$ está próximo de $x = 0$ pela direita.

2.

$\lim_{x \rightarrow 0^-}f(x) = +\infty(\text{infinito})$

Por outro lado, ao analisar o comportamento pela esquerda($0^-$), elevemos um número negativo ao quadrado, que o torna positivo, Tem-se p mesmo fenômeno quando $x > 0$, logo:

$\lim_{x \rightarrow 0^-}f(x) = \lim_{x \rightarrow 0^+}f(x) = +\infty$

DEFINIÇÃO:

Quando o limite lateral de uma função($x \rightarrow a^- ou x \rightarrow a^+$) é infinito, dizemos que a reta $x = a$ é uma $\color{red}\text{assíntota vertical}$ de $f(x)$. Por sua vez, pelo menos uma das seguintes condições deve ser satisfeita:

$\lim_{x \rightarrow a}f(x) = +\infty \text{ ou } -\infty$

$\lim_{x \rightarrow a^-}f(x) = +\infty \text{ ou } -\infty$

$\lim_{x \rightarrow a^+}f(x) = +\infty \text{ ou } -\infty$

EX:

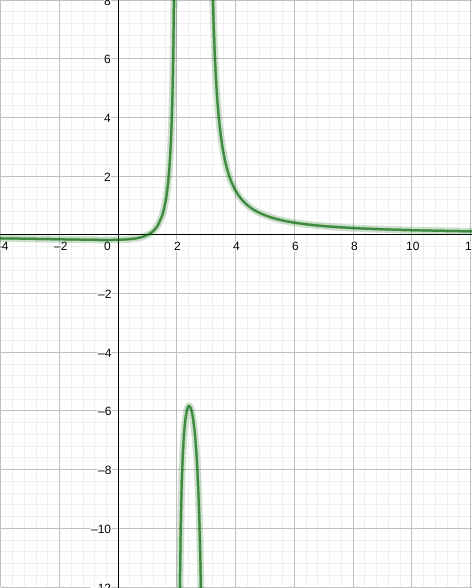
Verifique a função possuí assíntotas verticais:

$f(x) = \frac{x - 1}{x^2 - 5x + 6}$

---

$ x^2 - 5x + 6 \Rightarrow \Delta
\Delta = b^2 - 4ac \Leftrightarrow
\Delta = (-5)^2 - 4\cdot1\cdot6 \Leftrightarrow
\Delta = 25 - 24 \Leftrightarrow
\Delta = 1 $

$ x = \frac{-b \pm \sqrt\Delta}{2a} $

$ x_1 = \dfrac{5 + 1}{2} = 3 $

$ x_2 = \dfrac{5 - 1}{2} = 2 $

$ \lim_{x \rightarrow 2^-} f(x) = + \infty \lim_{x \rightarrow 2^+} f(x) = - \infty $

$ \lim_{x \rightarrow 3^+} f(x) = - \infty \lim_{x \rightarrow 3^-} f(x) = + \infty $

ATIVIDADE:

Encontrar a(s) assíntotas da função:

$f(x) = \frac{2x}{x-3}$

E determinar seus limites laterais.

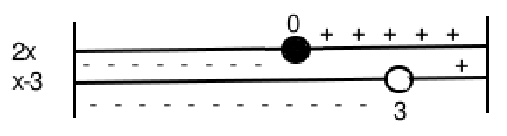
Assíntota em $x = 3$

$\lim_{x \rightarrow 3^-} = -\infty \lim_{x \rightarrow 3^+} = +\infty$

$\bold x$	$\bold {f(x)}$
$2$	$-4$
$2,5$	$-10$
$2,8$	$-28$
$2,9$	$-58$
$2,99$	$-598$
$2,999$	$-5998$

$\bold x$	$\bold{f(x)}$
$4$	$8$
$3,5$	$14$
$3,2$	$32$
$3,1$	$62$
$3,01$	$602$
$3,001$	$6002$