aula anterior | próxima aula

Digitado por $\color{black} \text{Diefesson de Sousa Silva - 471942}$

Derivadas e taxa de variação

DEFINIÇÃO: uma reta tangente a uma curva $y = f(x)$, com ponto $P(x, f(x))$ é uma reta que passa pelo ponto $P$ e que possui a inclinação $m$, tal que:

$ m = \lim_{x \rightarrow a} \left( \frac{f(x) - f(a)}{x - a} \right) $

Se o limite existir.

EXEMPLO: encontrar uma equação de reta tangente a curva $y = x^2$ no ponto $(1, 1)$:

$ \lim_{x \rightarrow 1} \left( \frac{x^2 - 1}{x - 1} \right) \Leftrightarrow $

$ \lim_{x \rightarrow 1} \left( \frac{(x + 1)(x - 1)}{x - 1} \right) \Leftrightarrow $

$ \lim_{x \rightarrow 1} \left( x + 1 \right) \Leftrightarrow $

$2$

Uma definição quando substituímos $x - a$ por $h$ e aproximamos $x \rightarrow a$, ou seja, $h \rightarrow 0$ e a inclinação $m$ da tangente é expressa por:

$ m = \lim_{h \rightarrow 0}\left( \frac{f(a + h) - f(a)}{h} \right) $

EXEMPLO: encontrar a reta tangente à curva $f(x) = \dfrac{3}{x}$ no ponto $(3, 1)$

$ \lim_{h \rightarrow 0} \left( \frac {\frac{3}{3+h} - \frac{3}{3}} {h} \right) \Leftrightarrow $

$ \lim_{h \rightarrow 0} \left( \frac {\frac{3}{3+h} - 1} {h} \right) \Leftrightarrow $

$ \lim_{h \rightarrow 0} \left( \left( \frac {3} {3+h} \right) \cdot \frac{1}{h} \right) \Leftrightarrow $

$ \lim_{h \rightarrow 0} \left( \frac {3-(3 + h)} {(3 +h)h} \right) \Leftrightarrow $

$ \lim_{h \rightarrow 0} \left( \frac {-h} {(3 +h)h} \right) \Leftrightarrow $

$ \lim_{h \rightarrow 0} \left( \frac {-1} {3 +h} \right) \Leftrightarrow $

$-\frac{1}{3}$

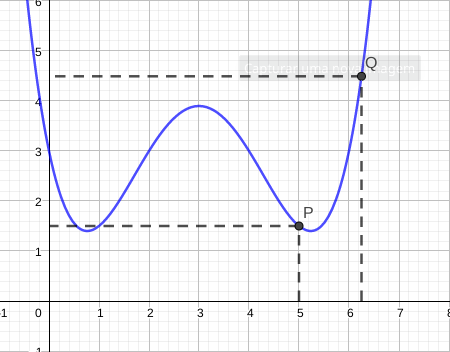
Interpretação geométrica

Ponto $P(x_0, y_0)$

Ponto $Q(a, f(a)) = (x_0 + h, y_0 + f(x+0 + h))$

Equação da reta:

$y-y_0 = m(x-x_0)$

$\text{ou}$

$m = \frac{y - y_0}{x - x_0}$

Derivadas

DEFINIÇÃO: a derivada de uma função $f$ em um número $a$ é determinada por $f’(a)$ e corresponde a:

$ f’(a) = \lim_{h \rightarrow 0} \left( \frac{f(a + h) - f(a)}{h} \right)= \lim_{x \rightarrow 0} \left( \frac{f(x) - f(a)}{x - a} \right) $

Podemos dizer então que a reta tangente a $y = f(x)$ no ponto $P(a, f(a))$ é a reta que passa em $a$ e que possuí inclinação $m$ igual a $f’(a)$ no ponto $a$.

De modo geral, podemos representar a equação da reta tangente na forma.

$y - f’(a) = f’(a) \cdot (x - a)$

Podemos dizer, também que $f’(a)$ representa a taxa de variação em uma função em um determinado ponto $P(a, f(a))$.

São válidas, portanto, as afirmações a seguir:

1. Se $f(x)$ é crescente na vizinhança de $a$ então $f’(a) > 0$.

2. Caso $f(x)$ seja decrescente, $f’(a) < 0$.

3. Se $f(x)$ tem ponto máximo ou ponto mínimo em $a$ ou $f(x)$ for constante, $f’(a) = 0$.